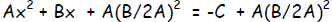Quadratic equations
| 3. | Solving Quadratic Equations by Completing the
Square—ANY quadratic equation can be solved by completing the square. The method works when the factors are not immediately obvious, making the equation difficult to factor. |
| Step 1: | Keep the x2 and x terms on one side
of the equation, and the constant term on the other. |
| Step 2: | Complete the square. If we have Ax2
+ Bx = -C complete its square by adding the constant A(B/2A)2 to both sides. |
| In other words, we complete the
square by taking ½ of B/A , squaring it and further scaling it by A. Be sure to add it to BOTH sides to keep the equation balanced.
|
|
| Step 3: | Factor the perfect square (created in step 2)
as a binomial squared : |
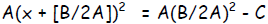 or dividing both sides by A: or dividing both sides by A: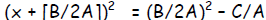 |
|
| Step 4: | Now we can solve the equation in step 3 by
using the square root method outlined previously. |
| Example 8: | Solve x2 - 8x = -11 by completing the square. |
| Step 1: | Keep the x2 and x terms on one side
of the equation, and the constant term on the other. Already done. |
| Step 2: | Complete the square. |
| Step 3: | Factor the perfect square (created in step 2)
as a binomial squared : |
| Step 4: | Now we can solve the equation in step 3 by
using the square root method outlined previously. |
| Example 9: | Solve 3x2 + 8x – 12 = 0 by completing the square. |
| Step 1: | Keep the x2 and x terms on one side
of the equation, and the constant term on the other. |
| Step 2: | Complete the square. For 3x2 +
5x = 12, A = 3 and B = 5. Thus,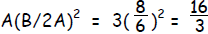 ( also ( also
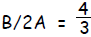 ) so, to keep the equation ) so, to keep the equationbalanced, |
| Step 3: | Step 3: Factor the perfect square (created in
step 2) as a binomial squared : |
| Step 4: | Now we can solve the equation in step 3 by
using the square root method outlined previously. |
| 4 | Solving Quadratic Equations by the Quadratic
Formula ANY quadratic equation can be solved by using the quadratic formula. If the factors do not immediately present themselves, this formula will nail them. |
| Step 1: | Simplify each side if needed. To remove
fractions: As fractions are another way to perform division, and the inverse of division is multiplication, you remove fractions by multiplying both sides by the least common denominator of all of your fractions. |
| Step 2: | Write in standard form, Ax2 +
Bx + C , if needed. If it is not in standard form, move any term(s) to the appropriate side by using the addition/subtraction property of equality. |
| Step 3: | Identify A, B, and C. When the quadratic
equation is in standard form, then A is the coefficient in front of the x2 term, B is the coefficient in front of the x term, and C is the constant term. |
| Step 4: | Use A, B, and C in the quadratic formula.
Roots 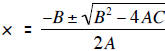 |
| Step 5: | Simplify if possible. |
| Example 10: | Solve 4x2 – 6 = 3x by using the quadratic formula. |
| Step 1: | Simplify each side if needed. No fractions, already simple |
| Step 2: | Write in standard form, if needed. |
| Step 3: | Identify A, B, and C. A = 4 B = -3 C = -6 |
| Step 4: | Use A, B, and C in the quadratic formula. |
| Step 5: | Simplify if possible. |
| Example 11: | Solve x(x + 2) = -10 by using the quadratic formula. |
| Step 1: | Simplify each side, if needed. |
| Step 2: | Write in standard form, if needed. |
| Step 3: | Identify A, B, and C. A = 1 B = 2 C = 10 |
| Step 4: | Use A, B, and C in the quadratic formula. |
| Roots x = | |
| Step 5: | Simplify if possible. |
| Example 12: | Solve by using the quadratic formula.
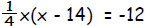 |
| Step 1: | Simplify each side, if needed. |
| Step 2: | Write in standard form, if needed. |
| Step 3: | Identify A, B, and C.
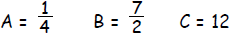 |
| Step 4: | Use A, B, and C in the quadratic formula. Roots x = |
| Step 5: | Simplify if possible. Multiply numerator and denominator by 2: |
Discriminant—When a quadratic equation is in
standard form, Ax2 + Bx + C,
= 0 the expression, B2- 4AC, that is found under the square root part
of the
quadratic formula is called the discriminant. The sign of the
discriminant
can reveal how many solutions there are going to be and if the solutions are
real numbers or complex numbers.
| When the Discriminant b2-4ac is |
Characteristic Solution |
Comment |
| > 0 | Two distinct real solutions |
As the discriminant is found under the square root, if its value is positive, then the quadratic possesses two distinct real roots |
| = 0 | One real solution |
As the discriminant is found under the square root, if its value is zero, then the quadratic possesses only one real root. |
| < 0 | Two distinct complex imaginary solutions |
As the discriminant is found under the square root, if its value is positive, then the quadratic possesses two distinct complex roots |
To determine the determinant, it is necessary to convert a
given trinomial
form to standard form. Then you can easily read off A, B and C.
For the following quadratics, determine the value of the discriminant and
give the number and type of roots:
(a) 2x2 – 8x + 7 discr. = 82 -
4(2)(7) = 64 - 56 = 8, >0,
(b) x2 + x - 1 discr. =
(c) x2 + 4x + 4 discr. =
(d) 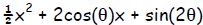 Determine over the entire domain 0
≤ θ ≤ ½π
Determine over the entire domain 0
≤ θ ≤ ½π
discrim = [2cos(θ)]2 – 4( ½)sin(2θ)
=
Now from a trigonometric identity:
Note that the discriminant is a function of θ. For some values of θ, it is
positive, for others it is negative. So, we must divide the domain into 3
regions:
Now for 0 < θ < 45°, cos(θ) > sin(θ), whereas for 45° < θ <90, cos(θ) < sin (θ).
Thus for 0 < θ < 45°.
When θ = 45°, cos(45°) = sin(45 °), thus
For 45° < θ < 90° cos(θ) < sin(θ) so
(e) 3x2 – 5x + 2
(f) x2 + 4 = 0 discr. =
(g) An alternate form of the quadratic equation is given by dividing all the
terms
the standard form of the quadratic equation by x2 to obtain;
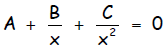
This form is helpful if B2 >> 4AC where denotes
much greater, in which case
the usual form of the quadratic formula can give inaccurate numerical results
for one of the roots. Show that it leads to the solution:
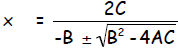
Solution. Let’s solve by completing the square:
Step 1: Keep the x -2 and x -1 terms on one side of the
equation, and the
constant term on the other. 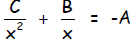
Step 2: Complete the square=
Inside the parentheses, take half of
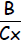 and square it, add result to both sides:
and square it, add result to both sides:
Step 3: Factor the perfect square (created in step 2)
as a binomial squared:
Divide by C :
Step 4: Now we can solve the equation in step 3 by using the square root
method outlined previously.
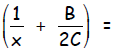 subtract
subtract
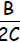 from both sides:
from both sides:
Finally, taking the inverse to recover x :
x =
Okay-eee, that should just about do it—Either you love quadratics more or
you loathe them more now.