Dividing Fractions

5. Jose and Mark are making cookies for a bake sale. Their recipe calls for 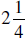cups of
flour for each batch. They have 5 cups of flour. Jose and Mark realize that they can make
two batches of cookies and that there will be some flour left. Since the recipe doesn’t call
for eggs, and since they have plenty of the other ingredients on hand, they decide they can
make a fraction of a batch in addition to the two whole batches. But Hose and Mark have a
difference of opinion. Jose says that 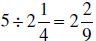, so he says that they can make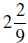
batches of cookies. Mark says that two batches of cookies will use up 4 ½ cups of flour
leaving ½ left, so they should be able to make 2 ½ batches. Mark draws the picture in
Figure 7.25 to explain his thinking to Jose. Discuss the boys’ mathematics: What’s right,
what’s not right, and why? If anything is incorrect, how could you modify it to make it
correct?

Jose doesn’t tell us his reasoning but his answer is right so I am not going to argue.

Mark, however, is confusing his wholes. 2 batches will indeed use up 4 ½ cups of sugar, as he
says, and that leaves ½ cup of sugar left. But ½ cup of sugar is not the same as ½ of a batch of
cookies. A batch of cookies requires 2 ¼ cups of sugar—not 1 cup—so the ½ cup of sugar
represents a lot less than ½ of a batch.

Mark’s picture seems to show one rectangle representing one cup of sugar. He’s marked off two
copies of 2 ¼, leaving ½ of a rectangle, which is ½ cup of sugar. Now how much of a batch of
cookies is that?

If we break up all of Mark’s big rectangles into four pieces (the way he did the middle
rectangle), each representing ¼ of a cup of sugar, then one batch of cookies requires 9 of those
small pieces. What we have left (out of our 5 cups of sugar) is only 2 of those pieces. Therefore
we have 2 pieces out of 9 that make a batch of cookies; so we can make 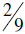of a batch of
cookies with what remains. Add that to the 2 batches we can make from the first 4 ½ cups of
sugar, and we get 2 and 2/9 batches of cookies.

10. Write a “how many groups?” story problem for ½ ÷ 2/3, and solve your problem in a
simple and concrete way without using the “invert and multiply” procedure. Explain your
reasoning. Verify that your solution agrees with the solution you obtain by using the
“invert and multiply” procedure.

My recipe for goose dumplings calls for cup of goose fat. Unfortunately my little goose
yielded only ½ of a cup of fat, so I can’t make the whole recipe. How much of a recipe can I
make?

We are not allowed to invert and multiply. Too bad; we’ll have to think it through. I notice that
my cup measure will measure down to sixths of a cup, so I have an idea. How many sixths of a
cup are these numbers? I have 1/2 of a cup of goose fat....that is 3 sixths of a cup of fat. The
recipe wants 2/3 cup of fat, which is 4 of those sixths...so I have 3 and the recipe wants 4...oh,
right; so I can only make 3/4 of a recipe. There! That wasn’t so hard.

17. Grandma’s favorite muffin recipe uses 1 ¾ cups of flour for one batch of 12 muffins.
For each of the problems (a) through (c), solve the problem in two ways: (1) by using
elementary reasoning about the story situation and (2) by interpreting the problem as a
division problem (say whether it is a “how many groups?” or a “how many in one group?”
type of problem) and by solving the division problem using standard paper and pencil
methods. Do not use a calculator. Verify that you get the same answer both ways.

a.) How many cups of flour are in one muffin?
(1) If there are 1 ¾ cups of flour in 12 muffins, there must be half of that in 6 muffins. Half of
1¾ is ½ of 7/4, which is ½ of 14/8, which is 7/8. If there are 7/8 cups of flour in 6 muffins, there
must be half of that in 3 muffins. Half of 7/8 is 7/16. Now, if there are 7/16 cups of flour in 3
muffins, there must be 1/3 of that in 1 muffin. So, the amount of flour in one muffin is 7/48 cups.
(2) This is a “how many in one group?” problem where muffins are the groups, and there are 1 ¾
cups of flour total in all the groups.

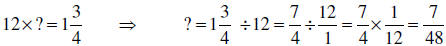
So, there are 7/48 cups of flour in each group (muffin).

b.) How many muffins does 1 cup of flour make?
(1) Well, 7/48 cups of flour makes 1 muffin, so 14/48 cups makes 2 muffins. But we have a lot
more flour than that, so we could make 6 muffins if we had 3 times that amount, which is 42/48
cup. Then we would have 6/48 of a cup leftover. That 6/48 of a cup is 6 of the 7 “48ths” that we
need to make another muffin. So, we could make 6 and 6/7 muffins from 1 cup of flour.
(2) This is a “how many groups?” problem with muffins as the group and 7/48 as the objects per
group.

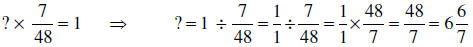
So, our answers in both parts are the same!

c.) If you have 3 cups of flour, then how many batches of muffins can you make? (Assume
that you can make fractional batches of muffins and that you have enough of all the
ingredients.)
(1) One batch calls for 1 ¾ cup of flour, so I know I have enough for one batch. Since 1 ¾ +1 ¾
is more than 3, I don’t have enough for two batches. After I use my 1 ¾ cup flour for the first
batch, I have 1 ¼ cups left. How many times does 1 ¾ fit into 1 ¼? Let’s try a smaller problem.
How many ¼ pieces are in 1 ¾? Well, that is 7. How many ¼ pieces are in 1 ¼? That is 5. So, I
have 5 of the 7 “1/4 pieces” that I need. So, in all I can make 1 and 5/7 batches.
(2) This is a “how many groups?” problem with batches as the groups and 3 cups of flour as the
total objects.

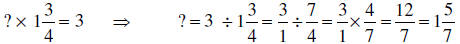
So, our answers in both parts are the same!

20. Write a “how many in one group?” story problem for 9 ÷ ¾, and use your story
problem to explain why it makes sense to solve 9 ÷ ¾ by “inverting and multiplying”—in
other words, by multiplying 9 by 4/3.

I used 9 cups of sugar to make some cookies. Actually, I only made ¾ of a recipe. How many
cups of sugar does my full recipe call for?

The equation would be
(number of recipes) × (number of cups in one recipe) = (number of cups used)
So we need to solve ¾ × ? = 9 .

If three-fourths of a recipe is 9 cups, then how many cups is one-fourth of a recipe?
Three of the fourths is 9, so one of the fourths is 3. So one fourth of a recipe is 3 cups. Now how
much is the whole recipe? Four of the fourths. One fourth is 3 cups, so four fourths is ... 12 cups.

Now we can see how the “invert and multiply” thing comes about. Three fourths of a recipe was
9. What was the first thing we did? We found one fourth. We knew how much 3 of something (a
fourth of a recipe) was; and we wanted to find out how much 1 of that same thing was. So we
divided by 3 to find out how much one-fourth was. Then we knew how much one-fourth of a
recipe was: namely 3 cups. To find out how much a whole recipe was, we needed to take four of
those fourths. So we multiplied by 4. So — to divide by 3/4 — we divided by 3 and then
multiplied by 4. That is the same as multiplying by 4/3.